# Python
x = -123
while x:
x >>= 1Pętla ta pojawiła się w książce “Zrozumieć Programowanie” Gynael Coldwinda z tym samym pytaniem, które znajduje się w tytule posta. Oczywiście moglibyśmy po prostu uruchomić powyższy kod i zobaczyć jego wynik jednak bardziej od wyniku ciekawsze jest to, co do niego doprowadziło.
Odpowiedź na zadane pytanie na pewno znają osoby, którym podstawy liczb binarnych nie są obce. Zdaje sobie sprawę, że jednak nie każdy musi je znać (o co swoją drogą toczyła się żywa dyskusja w tym wątku na Twitterze) i dlatego chciałbym pokrótce wyjaśnić zasadę działania tego kodu.
Jeżeli spojrzymy na tę pętlę, to widzimy, że jedyna akcja, która nią steruje to operator >>. Operator ten realizuje tak zwane przesunięcie bitowe, które jest ściśle związane z system binarnym i operacjami na bitach. Jeżeli nie znasz jeszcze systemu binarnego, to zachęcam do przeczytania kolejnego akapitu, gdzie robię błyskawiczne wprowadzenie. Znajomość tego systemu jest konieczna, aby zrozumieć zasadę działania omawianego kodu. Dla osób, które znają system binarny, polecam przeskoczyć do części Kod uzupełnień do dwóch (ZU2).
System binarny
Działanie komputera opiera się w głównej mierze na operacjach na bitach, które z kolei mogą reprezentować liczbę w postaci binarnej (inaczej dwójkowej). Zapis binarny jest systemem pozycyjnym, w którym wartość liczby obliczamy jako sumę potęg liczby 2 na poszczególnych pozycjach. Czyli liczby reprezentowane są za pomocą ciągów złożonych jedynie z dwóch znaków 0 i 1. Na bit 0 można mówić też zgaszony lub stan niski, a na 1 analogicznie — zapalony lub stan wysoki. Kiedy chcemy zapisać dziesiętną liczbę 23 w postaci binarnej, to będzie miała ona postać 10111 (w przypadku stałej liczby bitów np. 8 wartość ta będzie miała dodatkowe zera z lewej strony 00010111, które dla uproszczenia mogą być pomijane, gdyż nie mają wpływu na wynik) – można to sprawdzić na przykład za pomocą tego narzędzia.
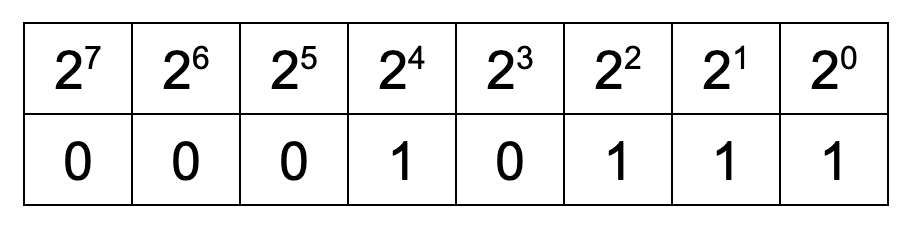
Z powyższego obrazka wynika że: (2^4 * 1) + (2^3 * 0) + (2^2 * 1) + (2^1 * 1) + (2^0 * 1) = 23.
Jest to po prostu suma potęg liczby 2 z miejsc w których występuje jedynka.
Mając do dyspozycji 8 bitów największa liczba jaką możemy zapisać to 255 czyli 11111111, a najmniejsza to 0 czyli 00000000.
Liczby naturalne zapisuje się właśnie w tej postaci i jest to dosyć prosta operacja. Ciekawiej się robi, kiedy musimy zapisać liczbę ujemną. Tutaj mamy dwie możliwości — albo możemy zapisać dodatkowy bit znaku, albo możemy zastosować kod uzupełnień do 2. W przypadku komputera częściej używana jest ta druga metoda, dlatego skupię się właśnie na niej.
Kod uzupełnień do dwóch (U2)
Kod uzupełnień do dwóch to metoda (inaczej U2 lub ZU2), która pozwala zapisać ujemne liczby w postaci binarnej. Metoda ta zakłada, że lewy skrajny bit wskazuje czy liczba jest dodatnia, czy ujemna. Kiedy bit ten ustawiony jest na 0 mamy do czynienia z liczbą dodatnią (lub zerem) i zapis tej liczby nie będzie się niczym różnił od normalnego zapisu liczby pokazanej w poprzednim akapicie. Kiedy jednak lewy skrajny bit ustawiony jest na 1 mamy do czynienia z liczbą ujemną. Aby uniknąć nieporozumień w interpretacji zapisu binarnego, kiedy będę reprezentował liczbę zapisaną w systemie ZU2 będzie ona oznaczona indeksem dolnym (U2) np. 1101(U2)
Kiedy chcemy zapisać liczbę -23 za pomocą systemu uzupełnień do dwóch na ośmiu bitach to musimy wykonać kilka kroków.:
- Zapisać liczbę 23 normalnie w postaci binarnej czyli
00010111 - Zamienić wartość bitów na przeciwne (tj. 0 na 1, 1 na 0) czyli
11101000 - Powiększyć liczbę (dodawanie binarne) o
1czyli11101001(U2)
W ten sposób otrzymaliśmy zapis 11101001(U2) , który reprezentuje liczbę -23. Można to sprawdzić tym samym kalkulatorem. Należy patrzeć na wynik w okienku Decimal from signed 2's complement.
Istnieje jeszcze drugi sposób, powiedziałbym, że bardziej manualny, ale w przypadku omawiania naszej pętli będzie dobrze go znać.
Na początku zapiszmy wartość początkową 10000000(U2), która reprezentuje liczbę -128 (2^7 = 128, ze znakiem minus to -128). Teraz gdy zapalimy prawy skrajny bit, to zapis 10000001(U2) oznacza liczbę -127 bo do -128 dodajemy 1. Gdy zapalimy kolejny bit, otrzymamy 10000011(U2) czyli -125.
Widać więc, że sposób ten sprowadza się do tego, aby do liczby -128 dodać sumę potęg liczby 2 z miejsc, gdzie występuje zapalony bit oczywiście z pominięciem lewego skrajnego bitu.
Warto zauważyć, że kiedy lewy skrajny bit jest zapalony i reprezentuje liczbę ujemną, to nie ma możliwości zapisania wartości 0, bo jeżeli zapalimy wszystkie bity 11111111(U2) to otrzymamy liczbę -1.
Czyli największa 8 bitowa liczba ujemna, jaką możemy uzyskać stosując ten systemem, to -128 czyli 10000000(U2), a największa -1 czyli 11111111(U2).
Aby dowiedzieć się więcej o zapisie binarnym polecam tę stronę
Przesunięcie bitowe
Przesunięcie bitowe (logical shift) to operator bitowy — jak sama nazwa wskazuje — do przesuwania bitów. Operator ten przesuwa wszystkie bity o n pozycji w lewo (operator <<) lub prawo (operator >>) i zazwyczaj wykorzystuje się go do szybkiego mnożenia lub dzielenia przez liczbę 2 i jej kolejnych potęg.
Mając naszą liczbę 23 zapisaną w postaci binarnej 00010111 przesunięcie bitowe w lewo << o jedną pozycję da nam wynik 00101110, co odpowiada liczbie 46 (została pomnożona przez 2). Czyli dopisane zostało jedno zero z prawej strony, a jedno zero z lewej strony zostało “ucięte”.
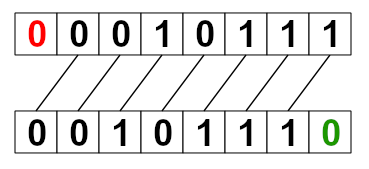
Analogicznie sytuacja ma się w przypadku przesunięcia bitowego w prawo >>. Przesunięcie o jedną pozycję da nam wynik 00001011, co odpowiada liczbie 11 (23/2 = 11.5 w tym przypadku zawsze zaokrąglamy w stronę zera). Dopisaliśmy więc zero z lewej strony, a prawa skrajna jedynka została “ucięta”.
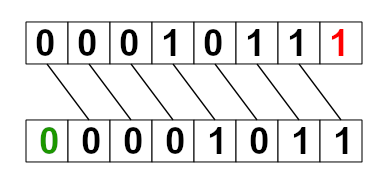
Tak działa to na liczbach dodatnich.
Kiedy jednak mamy do czynienia z liczbami ujemnymi, sytuacja się trochę zmienia, ale tylko i wyłącznie dla operacji przesunięcia bitowego w prawo.
Mając liczbę -23 11101001(U2) i wykonując operację przesunięcia bitowego w prawo opisaną wyżej, otrzymalibyśmy 01110100(U2) co reprezentuje liczbę 116. I z pomocą przychodzi arytmetyczne przesunięcie w prawo (arithmetic shift), które zamiast zer z lewej strony dopisuje wartość najbardziej znaczącego bitu, czyli w przypadku liczb ujemnych 1.
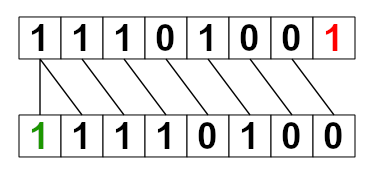
Czyli przesuwając jeden bit w prawo dla 11101001(U2) otrzymujemy 11110100(U2) , co daje nam -12 (liczby ujemne podczas tej operacji zaokrąglamy z dala od zera, w stronę ujemnej nieskończoności).
Operacje logicznego przesunięcia bitowego i arytmetycznego przesunięcia bitowego w prawo w niektórych językach programowania są reprezentowane za pomocą tego samego operatora >> i to język programowania decyduje którą operację wykonać, ale warto wspomnieć, że np. JavaScript wyróżnia specjalny operator >>> dla operacji logicznego przesunięcia w prawo.
Odpowiedź
Mając tę wiedzę możemy wrócić do pętli.
x = -123
while x:
x >>= 1
# Wyświetla postać binarną i decymalną
# print("{} ({})".format(format(x & 0xff, 'b'), x))
# Poczekaj sekundę, żeby widzieć wyniki na konsoli
# time.sleep(1)W każdym jej przebiegu następuje przesunięcie bitowe w prawo o jedną pozycję. Python jest jednym z języków, który ma tylko jeden operator przesunięcia bitowego w prawo i sam decyduje jaki mechanizm pod maską należy użyć. Mając więc do czynienia z liczbą ujemną, wykona arytmetyczne przesunięcie w prawo i dopisze 1 z lewej strony.
Jeżeli wyświetlimy liczby na konsolę ukaże się nam taki wynik:
11000010 (-62)
11100001 (-31)
11110000 (-16)
11111000 (-8)
11111100 (-4)
11111110 (-2)
11111111 (-1)
11111111 (-1)
11111111 (-1)
11111111 (-1)
...Jak wiemy liczba -1 jest najmniejszą wartością, jaką jesteśmy w stanie zapisać za pomocą kodowania U2, dlatego też każde kolejne przesunięcie bitowe w prawo nie zmienia już liczby i nigdy nie osiągnie ona innej wartości, a aby zakończyć pętlę wartość musiałaby być równa 0.
Jeżeli gdzieś się pomyliłem lub masz jakieś pytania czy uwagi – zapraszam do komentowania.
Do następnego!